树是一种重要的非线性数据结构，要求了解树形结构的特点，掌握树的定义、基本术语和性质，理解树中数据元素之间的关系。

1.树的定义和逻辑结构

（1）树的定义

树是n(n≥0)个结点的有限集T，n=0称为空树，n>0 为非空树。非空树中：

1.有且仅有一个称为根的结点；

2.当n>1时，其余结点可分为m个互不相交的有限集T₁、T₂、… 、T_m，而每一个T_i(i=1,2,…,m) 也是一棵树。T_i称为根的子树。

（2）树的逻辑结构

1.树中根结点的任意一个直接后继结点及该结点的所有后继结点也是以该结点为根的一棵树；

2.根结点没有前驱结点，其他结点有且仅有一个直接前驱结点；

3.每一个结点可以有零个或多个后继结点；

4.树型结构的元素间存在一对多的关系。

如图6-1所示的一棵树T。

它由根结点A和两棵子树T₁和T₂所组成，T₁和T₂分别位于A结点的左下部和右下部，其中树根结点A是两棵子树的根结点B和C的前驱，相反B和C是A的后继；

T₁又由它的根结点B和三棵子树T₁₁、T₁₂和T₁₃所组成，这三棵子树分别位于B结点的左下部、中下部和右下部，其中B结点是这三棵子树的根结点D、E和F的前驱，相反它们都是B的后继；T₁₁和T₁₃只含有根结点，不含有子树（或者说子树为空树），不可再分；T₁₂又由它的根结点E和两棵只含有根结点的子树所组成，每棵子树的根结点分别为H和I，E是H和I的前驱，而H和I均是E的后继；T₂由它的根结点C和一棵子树所组成，该子树也只含有一个根结点G，不可再分。

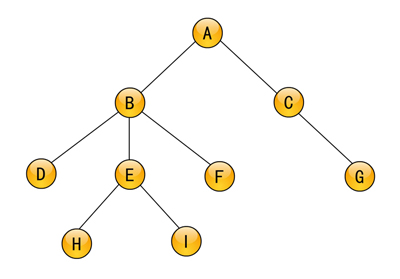
图6-1 树的逻辑结构

2.树的日常应用举例

在日常生活中，树结构广泛存在。

例6.1 可把一个家族看作为一棵树，树中的结点为家族成员的姓名及相关信息，树中的关系为父子关系，即父亲是儿子的前驱，儿子是父亲的后继。图6-2(a)就是一棵家族树，王庭贵有两个儿子王万胜和王万利，王万胜又有三个儿子王家新、王家中和王家国。

例6.2 可把一个地区或一个单位的组织结构看作为一棵树，树中的结点为机构的名称及相关信息，树中的关系为上下级关系。如一个城市分为若干个区，每个区又分为若干个街道，每个街道又分为若干个居委会等。

例6.3 可把一本书的结构看作为一棵树，树中的结点为书、章、节的名称及相关信息，树中的关系为包含关系。图6-2(b)是一本书的结构，根结点为书的名称数学，它包含三章，每章名称分别为加法、减法和乘法，加法一章又包含两节，分别为一位加和两位加，减法和乘法也分别包含若干节。

例6.4 可把一个算术表达式表示成一棵树，运算符作为根结点，它的前后两个运算对象分别作为根的左、右两棵子树。如把算术表达式a*b+(c-d/e)*f表示成树，则如图6-2(c)所示。

例6.5 在计算机领域，逻辑磁盘上信息组织的目录结构就是一棵树，树中的结点为包含有目录名或文件名的每个目录项或文件项，树中的根目录用反斜线表示，根目录下包含有若干个子目录项和文件项，每个子目录下又包含有若干个子目录项和文件项，依次类推。

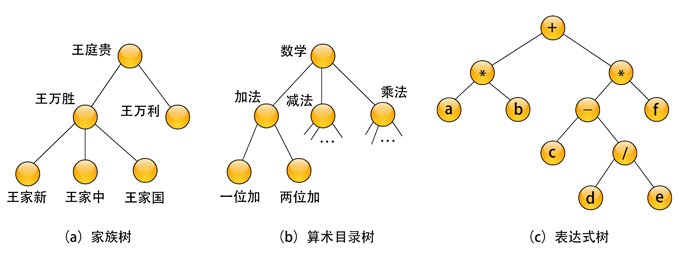
图6-2 树应用的例子

3.树的表示

树的表示方法有多种。图6-1和图6-2中的树形表示法是其中的一种，也是最常用的一种。在树形表示法中，结点之间的关系是通过连线表示的，虽然每条连线上都不带有箭头，但它并不是无向的，而是有向的，其方向隐含为从上向下，即连线的上方结点是下方结点的前驱，下方结点是上方结点的后继。树的另一种表示法是二元组表示法。对于图6-1所示的树T，若采用二元组表示，则结点的集合K和K上二元关系R分别为：

K={A,B,C,D,E,F,G,H,I}

R={<A,B>,<A,C>,<B,D>,<B,E>,<B,F>,<C,G>,<E,H>,<E,I>}

其中A结点无前驱结点，被称为树的根结点；其余每个结点有且仅有一个前驱结点；在所有结点中，B结点有三个后继结点，A结点和E结点分别有两个后继结点，C结点有一个后继结点，其余结点均没有后继结点。

除这两种之外，通常还使用广义表表示法，即每棵树的根作为由子树构成的表的名字而放在表的前面，图6-1树的广义表表示为：

A(B(D,E(H,I),F),C(G))

4.树的基本术语

（1）结点的度和树的度

一个结点的子树的数目或者说该结点引出的边数被定义为该结点的度（Degree）。树中所有结点的度的最大值被定义为该树的度。如在图6-1的树中，B结点的度为3，A、E结点的度均为2，C结点的度为1，其余结点的度均为0。因所有结点的最大的度为3，所以树的度为3。

（2）分支结点和叶子结点

在一棵树中，度等于0的结点称作叶子结点或终端结点，度大于0的结点称作分支结点或非终端结点。在分支结点中，每个结点的分支数就是该结点的度数，如对于度为1的结点，其分支数为1，又称为单分支结点；对于度为2的结点，其分支数为2，又称为双分支结点，其余类推。如在图6-1的树中，D、H、I、F、G为叶子结点；A、B、C、E为分支结点，其中C为单分支结点，A和E为双分支结点，B为三分支结点。

（3）孩子结点、双亲结点和兄弟结点

在一棵树中，每个结点的子树的根，或者说每个结点的后继，被习惯地称为孩子、儿子或子女（Child），相应地，把该结点称为孩子结点的双亲、父亲或父母（Parent）。具有同一双亲的孩子互称为兄弟（Brothers）。每个结点的所有子树中的结点被称为该结点的子孙。每个结点的祖先则被定义为从整个树的根结点到达该结点的路径上所经过的全部分支结点。如在图6-1的树中，B结点的孩子为D、E、F结点，双亲为A结点，D、E、F结点互为兄弟，B结点的子孙为D、E、H、I、F结点，I结点的祖先为A、B、E结点。对于图6-1树中的其他结点亦可进行类似的分析。

由孩子结点和双亲结点的定义可知：在一棵树中，根结点没有双亲结点，叶子结点没有孩子结点，其余结点既有双亲结点也有孩子结点。如在图6-1的树中，根结点A没有双亲，叶子结点D、H、I、F、G没有孩子，或者说孩子均为空。

（4）结点的层数和树的深度

 树既是一种递归结构，也是一种层次结构，树中的每个结点都处在一定的层次上。结点的层数（Level）从树根开始定义，根结点为第1层，它的孩子结点为第2层，以此类推。树中结点的最大层数被称为树的深度（Depth）或高度（Height）。如在图6-1的树中，A结点处于第1层，B、C结点处于第2层，D、E、F、G结点处于第3层，H、I结点处于第4层。H、I结点所处的第4层为图6-1树中结点的最大层数，所以此树的深度为4。

（5）有序树和无序树

若树中各结点的子树是按照一定的次序从左向右安排的，则称之为有序树，否则称之为无序树。如对于图6-3中的两棵树，若看作无序树，则是相同的；若看作有序树，则不同，因为根结点A的两棵子树的次序不同。又如，对于一棵反映父子关系的家族树，兄弟结点之间是按照排行大小有序的，所以它是一棵有序树。再如，对于一个机关或单位的机构设置树，若各层机构是按照一定的次序排列的，则为一棵有序树，否则为一棵无序树。因为任何无序树都可以当作任一次序的有序树来处理，所以以后若不特别指明，均认为树是有序的。

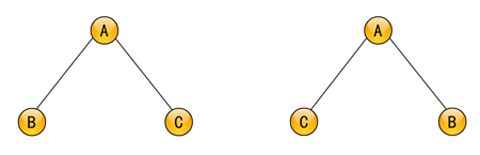
图6-3 两棵不同的有序树

（6）森林

森林是m(m≥0)棵互不相交的树的集合。例如，对于树中每个分支结点来说，其子树的集合就是森林。如在图6-1的树中，由A结点的子树所构成的森林为{T₁,T₂}，由B结点的子树所构成的森林为{T₁₁,T₁₂,T₁₃}，等等。

5.树的性质

性质1 树中的结点数等于所有结点的度数加1。

证明：

根据树的定义，在一棵树中，除树根结点外，每个结点有且仅有一个前驱结点，也就是说，每个结点与指向它的一个分支一一对应，所以除树根结点之外的结点数等于所有结点的分支数（即度数），从而可得树中的结点数等于所有结点的度数加1。

性质2 度为k的树中第i层上至多有k^i-1个结点（i≥1）。 >

下面用数学归纳法证明：

对于第一层显然是成立的，因为树中的第一层上只有一个结点，即整个树的根结点，而由i=1代入ki-1计算，也同样得到只有一个结点，即ki-1= k1-1=k0=1；假设对于第i-1层（i>1）命题成立，即度为k的树中第i-1层上至多有k(i-1)-1=ki-2个结点，则根据树的度的定义，度为k的树中每个结点至多有k个孩子，所以第i层上的结点数至多为第i-1层上结点数的k倍，即至多为ki-2*k= ki-1个，这与命题相同，故命题成立。

性质3 深度为h的k叉树至多有(k^h-1)/(k-1)个结点。

证明：

显然当深度为h的k叉树（即度为k的树）上每一层都达到最多结点数时，所有结点的总和才能最大，即整个k叉树具有最多结点数。

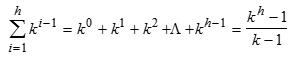
当一棵k叉树上的结点数等于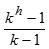时，则称该树为满k叉树。例如，对于一棵深度为4的满二叉树，其结点数为24-1，即15；对于一棵深度为4的满三叉树，其结点数为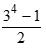，即40。

性质4：具有n个结点的k叉树的最小深度为[log_k(n(k-1)+1)]

证明：

设具有n个结点的k叉树的深度为h，若在该树中前h-1层都是满的，即每一层的结点数都等于ki-1个（1≤i≤h-1），第h层（即最后一层）的结点数可能满，也可能不满，则该树具有最小的深度。根据性质3，此树的结点数n必然小于等于高度为h的满k叉树的结点数，同时必然大于高度为h-1的满k叉树的结点数，则深度h与n之间的关系为：

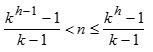
可变换为 k^h-1<n(k-1)+1≤k^h

以k为底取对数后得 h-1<log_k(n(k-1)+1)≤h

即 log_k(n(k-1)+1)≤h<log_k(n(k-1)+1)+1

因h只能是整数，所以 h=logk(n(k-1)+1)

因此得到具有n个结点的一般k叉树的最小深度为log_k(n(k-1)+1)。

注：x表示对x进行向上取整，其值为大于等于x值的最小整数。如x的值为4和4.3时，向上取整结果分别为4和5。与此相反，x表示对x进行向下取整，其值为小于等于x值的最大整数。如x的值为4.6和5时，向下取整结果分别为4和5。

例如，对于二叉树，求最小深度的计算公式为log2(n+1)，若n=20，则最小深度为5；对于三叉树，求最小深度的计算公式为log3(2n+1)，若n=20，则最小深度为4。